![]()
Editor de cristales de Bravais
Visor de planos cristalográficos
El visualizador de moléculas permite que el usuario pueda ver moléculas tridimensionales, debiendo para ello introducir un fichero con la estructura de la molécula. El visualizador trabaja en el supuesto que todas las moléculas estén formadas por dos componentes, átomos y enlaces. Cuando el visualizador muestre un átomo lo representará como una esfera de un color, determinado por un fichero de configuración y de esta manera cada elemento químico tendrá un color diferente.
Existen distintos tipos de enlaces químicos (enlace iónico, covalente, metálico, etc.) que mantienen unidos los átomos que forman la molécula. En todos los casos el enlace es una fuerza que une átomos y por tanto si pudiésemos ver a simple vista una molécula sólo veríamos los átomos mientras que los enlaces serían invisibles. El visualizador representa un enlace dibujando un cilindro entre los átomos que comparten el enlace.
La aplicación permite además configurar el visualizador de tal manera que el usuario puede escoger entre diversas opciones. Podemos representar una molécula viendo sólo los enlaces, los enlaces y los átomos o sólo los átomos. También podemos manipular una molécula trasladándola, girándola, haciendo zoom, etc.
Si miramos la definición de cristal en un diccionario dice:
Los cristales son una disposición periódica de átomos o moléculas en el espacio, en el que hay puntos en los que un observador está rodeado por el mismo número y tipo de átomos. Los cristales poseen simetría traslacional, esto significa que desde cualquier punto del cristal podemos llegar a otro punto, que no se diferencia del anterior. Es decir, el entorno de cada punto de la red es idéntico para cualquier traslación.
La definición es más completa si se añade que los cristales están constituidos por dos elementos, por una parte la estructura regular, o red regular, de puntos en el espacio y por otro lado el motivo, el conjunto de átomos o moléculas que se repiten en cada uno de estos puntos reticulares. Para ver un ejemplo ver la figura 1. La cristalografía es la ciencia que estudia los diferentes tipos de estructuras.
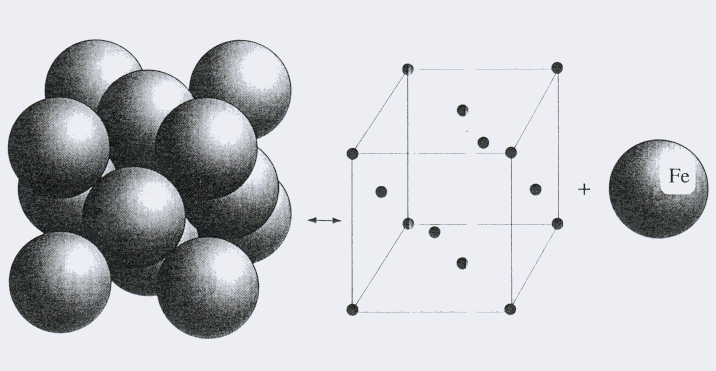
Figura 1: En este caso la red se conoce como Cúbica centrada en las caras (fcc), y el motivo es el átomo de hierro (Fe).
El Editor de cristales permite al usuario escoger el tipo de estructura, mostrándola inicialmente vacía para que se pueda insertar en ella el motivo deseado.
El número total de redes posibles en tres dimensiones se puede reducir a 14, las llamadas Redes de Bravais y todas ellas con sus variantes pueden ser visualizadas en la aplicación. Además hemos incluido algunas estructuras básicas adicionales bajo el epígrafe de Cristales simples, por la importancia que ostentan. Por ello, la aplicación tendrá dos editores, el Editor de cristales de Bravais y el Editor de cristales simples respectivamente.
Editor de cristales de Bravais
Como hemos dicho antes, las redes cristalinas corresponden a una disposición de puntos en el espacio con la propiedad de tener simetría traslacional. Esto quiere decir que cada punto de la red se puede obtener de otro punto mediante una traslación.
Las redes cristalinas se pueden racionalizar introduciendo el concepto de celda unitaria, la cual es un paralelepípedo que por traslación de sí mismo genera completamente la red cristalina.
Una celda unitaria se caracteriza por tres vectores que definen las tres direcciones independientes del paralelepípedo. Esto se traduce en seis parámetros de red, que son los módulos, a, b y c, de los tres vectores, y los ángulos ab y l que forman entre sí, como se muestra en la figura 2. Estos tres vectores forman una base del espacio tridimensional, de tal manera que las coordenadas de cada uno de los puntos de la red se pueden obtener a partir de ellos por combinación lineal con los coeficientes enteros.
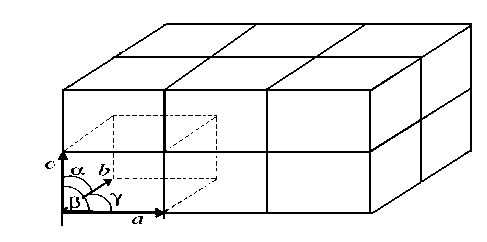
Figura 2: La celda unitaria aparece con líneas discontinuas.
En los cristales existen únicamente 32 clases de redes diferentes. Este es el resultado de buscar todas las simetrías posibles en que los puntos de una red se pueden agrupar de forma que sean compatibles con la existencia de un cristal.
Al establecer las restricciones de simetría que ha de obedecer la métrica para cada una de las 32 clases de simetría se observa que existen 7 conjuntos de parámetros de redes diferentes. Estos parámetros permiten clasificar las 32 clases de cristales en siete sistemas cristalográficos:
Sistema cúbico: a = b = c a = b = g = 90º
Sistema hexagonal: a = b ¹ c a = b = 90º g = 120º
Sistema tetragonal: a = b ¹ c a = b = g = 90º
Sistema Trigonal (*): a = b = c a = b = g ¹ 90º
Sistema ortorrómbico: a ¹ b ¹ c a = b = g = 90º
Sistema monoclínico: a ¹ b ¹ c a = g = 90º b ¹ 90º
Sistema triclínico: a ¹ b ¹ c a ¹b¹ g
* También se le conoce como Sistema Rómbico.
Las celdas que únicamente tienen puntos reticulares en los vértices del paralelepípedo se denominan celdas primitivas o simples y se denotan con la letra P. Las celdas centradas en las caras, que se escriben con la letra F, tienen puntos reticulares en los vértices del paralelepípedo y en el punto medio de cada cara. Las celdas con puntos situados en las bases, estas se denominan A, B, C según sean las caras que tienen los dos puntos reticulares. Y las celdas centradas en el cuerpo tienen los puntos reticulares en los vértices del paralelepípedo y otro punto reticular en el interior de la celda unitaria, a distancia equidistante a todos los vértices, y se escriben con la letra I.
Así pues, si hay siete sistemas cristalográficos y cuatro tipos diferentes de celdas unitarias deberían existir 28 redes diferentes. En realidad, el número total de redes posibles se reduce a 14 y son conocidas como Redes de Bravais. Se puede demostrar que cualquier red no incluida se puede reducir a una de las catorce.
Redes de Bravais
| Sistema | P | F | I | C (*) |
| Cúbico | Sí | Sí | Sí | |
| Hexagonal | Sí | |||
| Tetragonal | Sí | Sí | ||
| Trigonal | Sí (**) | |||
| Ortorrómbico | Sí | Sí | Sí | Sí |
| Monoclínico | Sí | Sí | ||
| Triclínico | SÍ |
* Faltaría incluir los tipos centrados en la cara A y B, pero ambos se pueden reducir de tipo C.
* * Este tipo se conoce como Trigonal R.
Las estructuras cristalinas simples que se estudiarán son: Cloruro de sodio, Cloruro de cesio, Hexagonal compacta, Diamante y Sulfuro de Zinc.
Estructura del Cloruro de Sodio
(NaCl)
La red del Cloruro de sodio está basada en la red cúbica centrada en las caras y el motivo es un átomo de Sodio (Na) y un átomo de Cloro (Cl) separados por ½ de la diagonal de una celda cúbica (ver figura 3). Hay cuatro unidades de NaCl en cada unidad cúbica.
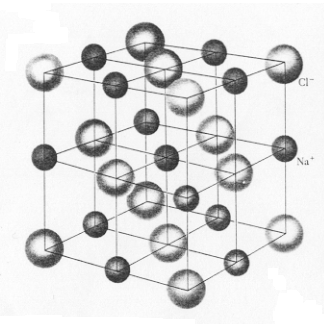
Figura 3: En este cristal existen ocho celdas unitarias (2x2x2)
Cada átomo tiene como vecinos más próximos seis átomos de la clase opuesta. Algunos cristales que tienen la misma disposición que el NaCl se pueden ver en la siguiente tabla:
| Cristal | a (Å) | Cristal | a(Å) |
| LiH | 4,08 | AgBr | 5,77 |
| MgO | 4,20 | PbS | 5.92 |
| MnO | 4,43 | KCl | 6,29 |
| NaCl | 5,63 | KBr | 6.59 |
El parámetro a representa el valor de la arista del cubo en angstrom: 1 Å º 10-10 m
Estructura del Cloruro de Cesio
(CsCl)
La estructura del Cloruro de cesio se puede ver en la figura 4. Hay una molécula por cada celda primitiva, con átomos en las esquinas y en el interior a partir de una red cúbica primaria, también conocida como cúbica I. Cada átomo puede ser visto como el centro de un cubo de átomos de la clase opuesta, así el número de sus vecinos más próximos son de 8. Las siguientes moléculas tienen la misma estructura:
| Cristal | a (Å) | Cristal | a (Å) |
| BeCu | 2,70 | LiHg | 3,29 |
| AlNi | 2,88 | NH4Cl | 3,87 |
| CuZn (b -brass) | 2,94 | TlBr | 3,97 |
| CuPd | 2,99 | CsCl | 4,11 |
| AgMg | 3,28 | TlI | 4,20 |
El parámetro a representa el valor de la arista del cubo en angstrom.
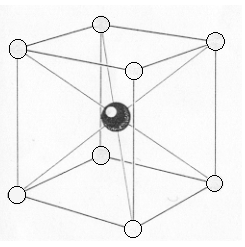
Figura 4
(hcp)
Hay un número infinito de maneras de disponer esferas idénticas de una forma regular que maximice el espacio compartido. Una de ésas es la estructura cúbica centrada en las caras, también conocida como fcc, la otra es el estructura hexagonal compacta o hcp. La fracción de volumen total ocupado por las esferas es 0,74 por ambas estructuras. Otras disposiciones que no sean estructuras, regulares o no, pueden llegar empaquetarse más densas, pero ya no serían cristales sólidos.
Para poder distinguir en que se diferencian las estructuras fcc y hcp ver la figura 5 y figura 6.
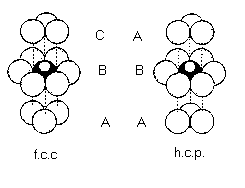
Figura 5: Como se puede ver se distinguen por la disposición de las capas A y C respecto la del centro, B.

Figura 6: En este gráfico vemos como se puede obtener la estructura compacta a partir de las celdas unitarias.
La estructura hcp viene dada por dos parámetros, el parámetro a corresponde a la base del hexágono y el parámetro c indica la altura, tal como se ve en la figura 7. El valor c/a para la estructura hcp es igual a 1.633 aunque también se llaman cristales hcp aquellos en que este valor es ligeramente distinto.
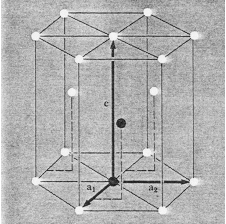
Figura 7
El número de vecinos inmediatos de un átomo cualquiera es de doce tanto en los hcp como en los fcc. En la siguiente tabla aparecen los elementos que se estructuran como hcp:
| Cristal | c/a | Cristal | c/a | Cristal | c/a |
| He (Helio) | 1,633 | Zn (Cinc) | 1,861 | Zr (Circonio) | 1,594 |
| Be (Berilio) | 1,581 | Cd (Cadmio) | 1,886 | Gd (Gadolinio) | 1,592 |
| Mg (Magnesio) | 1,623 | Co (Cobalto) | 1,622 | Lu (Lutecio) | 1,586 |
| Ti (Titanio) | 1,586 | Y (Itrio) | 1,570 |
La estructura del Diamante está basada en la red cúbica centrada en las caras o fcc. La celda primitiva consiste en dos redes fcc, la primera centrada en el punto (0,0,0), y la segunda está centrada en el (¼,¼ ,¼), o sea que está desplazada ¼ respecto la diagonal del cubo de la primera red.
La característica de la estructura del Diamante es el enlace tetraédrico, en el cual cada átomo está enlazado con otros cuatro átomos vecinos. La estructura del Diamante está relativamente vacía, la máxima proporción de espacio ocupado por esferas sólidas es 0,34, lo cual representa un 46% del espacio ocupado por las estructuras hcp o fcc. En la siguiente tabla aparecen elementos con estructura del Diamante.
| Cristal | a (Å) | Cristal | a (Å) |
| C (Carbono) | 3,56 | Ge (Germanio) | 5,65 |
| Si (Silicio) | 5,43 | Sn (Estaño) | 6,46 |
Aquí el parámetro a corresponde a la arista de la celda cúbica.
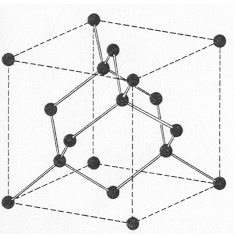
Figura 8
Estructura del Sulfuro de Zinc
(ZnS)
La estructura de Sulfuro de Zinc tiene la misma celda primitiva que la del Diamante, es decir, dos fcc’s donde la segunda fcc está desplazada ¼ de la diagonal del cubo. La diferencia estriba en el motivo, ya que si en la estructura diamantina todos eran iguales, en el Sulfuro de Zinc el primer fcc contiene únicamente átomos de Zn y el segundo fcc contiene sólo átomos de S. Hay cuatro moléculas de ZnS por cada celda primitiva. Cada átomo tiene cuatro átomos vecinos de la clase opuesta dispuestos en las esquinas de un tetraedro regular, tal como se puede ver en la figura 9. Ejemplos de estructuras cúbicas de Sulfuro de cinc son:
| Cristal | a (Å) | Cristal | a (Å) | Cristal | a (Å) |
| CuF | 4,26 | AlP | 5,45 | AlAs | 5.66 |
| SiC | 4,35 | GaP | 5,45 | CdS | 5,82 |
| CuCl | 5,41 | ZnSe | 5,65 | InSb | 6,46 |
| ZnS | 5,41 | GaAs | 5,65 | AgI | 6,47 |
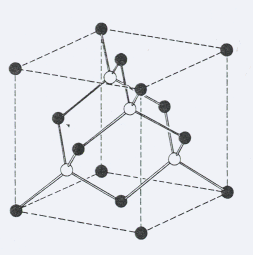
Figura 9
Visor de Planos cristalográficos
Los planos cristalográficos se denotan por los índices de Miller. Estos índices corresponden a los inversos de los puntos de corte del plano que queremos caracterizar con cada uno de los ejes de coordenadas, y se representan entre paréntesis sin comas (hkl). Los índices de Miller pueden representar a un plano o a toda una familia de planos paralelos que tienen la misma orientación. Para calcular los índices de Miller hemos de hacerlo siempre sobre un plano de la familia que no pase por el origen.
Como ejemplo encontraremos los índices del plano XY. Este plano no corta ni el eje X ni el eje Y, los corta en el infinito, en cambio el eje Z lo corta, por ejemplo en el 1. Entonces los índices de Miller para el plano XY son (hkl) = (1/¥ 1/¥ 1/1) = (001).
Para que la imagen quede clara, en el Visor de Planos cristalográficos se ha escogido la opción de que los índices de Miller sólo representen uno de los infinitos planos posibles. Dicho plano es mostrado mediante los átomos del cristal incluidos en él.Los planos sólo tienen utilidad cuando hablamos de cristales, por lo tanto esta funcionalidad sólo estará activa si lo queremos aplicar a cristales.
En la figura 10 podemos ver unos ejemplos.
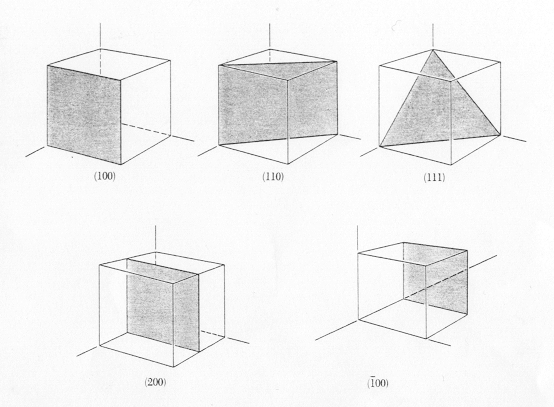
Figura 10: Los planos (100) y (200) son paralelos pero en el primero los puntos de corte son (1,¥ ,¥ ) y el segundo son (0.5,¥ ,¥ ).