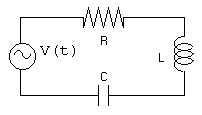
FUNDAMENTOS FISICOS
en los cuales se basan los applets.
Cuando una fuente de tensión alterna que suministra una diferencia de potencial (expresada en notación compleja)
`V(t) = Vo· eiwt
(Vo es la amplitud de la tensión y w = 2p f, siendo f la frecuencia) se conecta a un circuito RLC en serie, la intensidad que circula viene dada por la Ley de Ohm compleja
`I(t) = `V(t) /`Z,
donde
`Z = R + iC = R + i(Lw - 1/Cw)
es la impedancia de la carga y
C = (Lw - 1/Cw)
se denomina reactancia.

figura 1.
Si expresamos la impedancia y la diferencia de potencial en forma polar,
` Z = Z eij y ` V(t) = Voeiwt
entonces
`I(t) = Voeiw t / Z eij º Ioei(w t-j )
Io = Vo/Z
Z = (R2+ C 2)1/2
donde podemos observar que, en general la intensidad estará desfasada respecto la tensión en un ángulo j . El ángulo de desfasamiento satisface
tan j = (Lw - 1/Cw ) / R.
El coseno del ángulo,
cos j = R / Z,
es el factor de potencia del circuito.
Si j > 0 (j < 0) decimos que la I retrasa (avanza) respecto de V. Fijarse como se traduce este convenio cuando se visualizan señales alternas en función del tiempo. Si utilizamos la representación senos (cogemos la parte imaginaria de las magnitudes complejas), la magnitud que retrasa la veremos más a la derecha que la magnitud avanzada. Por ejemplo, si tuviésemos j = + p /2 y representamos la tensión (proporcional a la función sin(x), línea roja en la figura 2) y la intensidad (proporcional a sin(x - p /2), línea verde) en función de x = w t, veremos que la magnitud retrasada, I, está desplazada respecto de la otra, V, hacia la derecha. Fijarse que el ángulo de desfasamiento puede calcularse a partir de la gráfica. Hay que recordar que la distancia D entre dos máximos consecutivos de una función seno corresponde a un desfasamiento de 2p radianes. Podemos medir D en la gráfica, al igual que la distancia entre los máximos de dos señales sinusoidades, l. El desfasamiento j entre estos lo calcularemos a partir de una regla de tres: j / l = 2p / D.
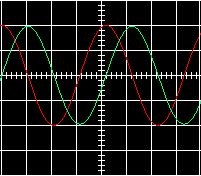
Figura 2.
Notar que la impedancia ` Z tiene, en general, un valor complejo, que depende de R, L, C y w .
Se denomina frecuencia de resonancia, f r, la frecuencia del señal alterno que hace que la impedancia del circuito sea sólo real, ` Z = R, es decir, con reactancia
C = (Lw -1/Cw ) = 0.
Que ` Z =R sea real, implica que ` V y` I están en fase. En estas condiciones, en un osciloscopio de 2 canales (mínimo) con la función de composición de gráficas (X-Y), y conectando uno de los canales a extremos de la fuente, y el otro a extremos de la resistencia y apretando el botón X-Y del osciloscopio, observaríamos en la pantalla una línea. Si no hay resonancia, obsevaríamos una elipse.
Se puede comprobar que
f r = w r / 2p = 1 / (2p (LC)1/2 ).
Para la frecuencia de resonancia, el módulo de la impedancia adopta el valor mínimo, lo que se traduce en que la amplitud de la intensidad que circula por el circuito sea máxima.
Las expresiones anteriores corresponden a un circuito RLC serie. Son también aplicables a circuitos serie RC (poniendo L=0), RL (poniendo C® ¥ ) y LC (poniendo R=0). La Ley de Ohm nos permite relacionar la tensión a extremos de cualquier elemento del circuito con la impedancia y la intensidad que circula:
|
` VR(t) = ` ZR`I(t), | ` ZR = R | |||||||||||||
| ` VL(t) =` ZL`I(t), | ` ZL = iLw = Lw eip /2 | ||||||||||||||
| ` VC(t) =` ZC`I(t), | ` ZC(t) = -i/Cw = (1/Cw) e-ip /2 |
Si conectamos un canal del osciloscopio a bornes de un elemento, podremos observar ( en la pantalla del osciloscopio) la tensión instantánea aplicada al elemento. Por ejemplo, si el elemento es la resistencia R, podremos saber fácilmente cual es la intensidad que circula, sólo dividiendo por el valor R. Si utilizamos las dos sondas disponibles conectándolas a los bornes de dos elementos diferentes, podremos observar los dos señales simultáneos, lo que nos permitirá encontrar su desfasamiento relativo.