TEORÍA FÍSICA EN LA QUE SE FUNDAMENTA LA REALIZACIÓN DEL PROYECTO
![]()

PRIMER APPLET :
Simulación de la trayectoria que sigue una partícula cargada con una cierta velocidad inicial, dentro de un campo eléctrico uniforme generado por un condensador plano.
![]()
1.- LEY DE COULOMB.
La fuerza ejercida por una carga puntual sobre otra está dirigida a lo largo de la línea que las une. La fuerza es inversamente proporcional al cuadrado de la distancia que separa las cargas y es proporcional al producto de estas. La fuerza es repulsiva si las cargas tienen el mismo signo y es atractiva si las cargas tienen signos opuestos.
Nota : los símbolos en negrita indican que son vectores.
La ley de Coulomb puede formularse sencillamente mediante la siguiente expresión matemática :
F12 = K · q1 · q2 · r12 / r123
Donde q1 y q2 son dos cargas puntuales separadas por una distancia r12 y K es la constante de Coulomb que tiene el valor :
K = 8,99 · 109 N·m²/C².
2.- EL CAMPO ELÉCTRICO.
Una forma de interpretar la ley de Coulomb consiste en la introducción del concepto de campo eléctrico. En el caso anterior diríamos que la carga q1 crea un campo eléctrico en todos los puntos del espacio y que este campo ejerce una fuerza sobre la carga q2 . Es decir :
E = K · q1· r12 / r123
F12 = q2 · E
El campo eléctrico es una representación de la fuerza ejercida por un conjunto de cargas sobre una carga de prueba q :
E = F / q
donde F es la fuerza ejercida y q la carga de la partícula de prueba. En el Sistema Internacional (S.I.) la fuerza se expresa en newtons (N) y la carga en Culombios (C), por lo que la unidad del campo eléctrico E será N/C.
3.- EL CAMPO ELÉCTRICO DEBIDO A UNA DISTRIBUCIÓN DE CARGAS PUNTUALES.
En el caso en que tengamos una distribución de cargas puntuales, el campo eléctrico resultante debido a esta distribución sera la suma de los campos eléctricos originados por cada carga por separado :
ET = E1 + E2 + E3 + ... + En
4.- LAS LÍNEAS DE CAMPO ELÉCTRICO.
El vector campo eléctrico es tangente a la línea en cada punto e indica la dirección del campo eléctrico en dicho punto. El campo eléctrico se suele representar como líneas de campo eléctrico o también llamadas líneas de fuerza. Estas líneas de fuerza tienen una serie de propiedades:
Las líneas de fuerza van siempre de las cargas positivas a las cargas negativas ( o al infinito ).
Las líneas siempre salen/entran simétricamente de las cargas.
El número de líneas de fuerza es siempre proporcional a la carga.
La densidad de líneas de fuerza en un punto es siempre proporcional al valor del campo eléctrico en dicho punto.
Por ejemplo, en los puntos cercanos a una carga positiva, el campo eléctrico apunta radialmente alejándose de la carga. Las líneas de campo eléctrico divergen desde el punto donde se encuentra la carga positiva.
En el siguiente dibujo podemos ver como las líneas de campo eléctrico se alejan de la carga puntual positiva, nótese también que a medida que nos alejamos de la carga positiva las lineas de campo se van separando, esto nos indica que el campo eléctrico va disminuyendo.
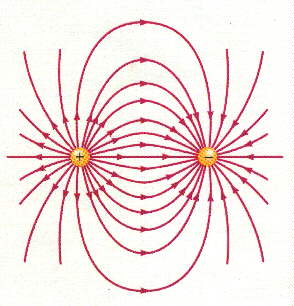
En este otro dibujo podemos ver como se forman las líneas de campo eléctrico en un dipolo. Como las dos cargas tienen el mismo valor el número de líneas de campo que salen de la carga positiva es igual al número de líneas que llegan a la carga negativa.
Nótese también que la densidad de líneas de campo es mayor entre las cargas que en los extremos exteriores a ellas, ello es debido a que el campo eléctrico formado en la zona que hay entre las dos cargas es mucho más intenso que en otra región.
5.- EL CONDENSADOR COMO GENERADOR DE UN CAMPO ELÉCTRICO CONSTANTE.
Un condensador de placas paralelas (plano) consiste en un par de placas conductoras cargadas uniformemente con signo diferente. El campo eléctrico entre placas es aproximadamente constante.
Cuando se coloca una partícula cargada en un campo eléctrico ésta experimenta la acción de una fuerza que es igual al producto de la carga de la partícula y el valor del campo eléctrico en el cual se ha introducido (F=q·E). La partícula con carga q adquiere una aceleración debida a la ley de la dinámica F=m·a , y tenemos que ésta tiene un valor de :
q · E = m · a
a = q · E / m
y sabemos también que si E es constante la partícula describirá un movimiento en forma de parábola.
![]()
SEGUNDO APPLET :
Simulación de la trayectoria que sigue una partícula cargada con una cierta velocidad inicial, dentro de un campo eléctrico uniforme generado por un condensador plano.
Modelo interactivo con resolución numérica.
![]()
En este modelo interactivo del primer applet, dados los valores necesarios para realizar la simulación se consigue a la vez ver la simulación y obtener unos datos numéricos reales sobre posiciones y velocidades de la partícula al atravesar y chocar con alguna de las placas del condensador.
Nota : los símbolos en negrita indican que son vectores.
La partícula describe un movimiento rectilíneo y uniforme antes de entrar en el condensador debido a la inexistencia de campo eléctrico fuera del condensador.
Si E = 0
No existe F = q · E
No existe aceleración.
Las ecuaciones de posición de la partícula serán :
X = Xo + vox · t = Xo + vo · cos ß · t
Y = Yo + voy · t = Yo + vo · sin ß · t
donde ß es el ángulo formado con la horizontal.
La partícula describirá un movimiento uniformemente acelerado al entrar en el interior del condensador, debido a que estará bajo la influencia del campo eléctrico uniforme generado por el condensador.
Si E # 0
Existe F = q · E
Existe aceleración, a = q · E/ m
Si el campo eléctrico está orientado según el eje 'y' entonces las ecuaciones de posición de la partícula serán :
X = Xo + vox · t = Xo + vo · cos ß · t
Y = Yo + voy · t + q·E / 2m · t2 =
= Yo + vo · sin ß · t + q·E / 2m · t2
donde el campo eléctrico será : E = V/d ,
donde d es la separación entre placas,
y donde ß será el ángulo formado con la horizontal.
La partícula describirá otra vez un movimiento rectilíneo y uniforme tras atravesar el condensador, debido también a la inexistencia de campo eléctrico fuera del condensador.
Si E = 0
No existe F = q · E
No existe aceleración.
Hay que hacer notar que sólo la componente 'y' del movimiento de la partícula se ve afectada por el campo eléctrico del condensador. Por tanto, la forma de la trayectoria dentro del condensador será muy parecida a la del tiro parabólico donde la fuerza de la gravedad es la protagonista del diseño de la parábola.
![]()
TERCER APPLET :
Simulación de la trayectoria que sigue una partícula cargada con una cierta velocidad inicial al entrar en un campo magnético uniforme y perpendicular al plano de la trayectoria.
![]()
1.- LA FUERZA EJERCIDA POR UN CAMPO MAGNÉTICO.
Nota : los símbolos en negrita indican que son vectores.
Cuando una carga q con una velocidad v está en una región donde hay un campo magnético, aparece una fuerza que depende de q y de v. A esta fuerza se le llama fuerza magnética y viene definida por la siguiente expresión :
Fm = q · v × B
( × es el signo del producto vectorial )
donde B es el campo magnético.
Algunas características de la fuerza magnética son :
- La fuerza magnética es proporcional a la carga q.
- La fuerza magnética es proporcional al módulo de la velocidad v.
- La fuerza magnética es perpendicular al plano definido por los vectores de campo magnético y velocidad.
- La fuerza magnética es proporcional al seno del ángulo formado por los vectores de velocidad v y campo magnético B. En el caso de que este ángulo fuera cero, o sea que los dos vectores fueran paralelos, la fuerza magnética sería nula.
En resumen, cuando una carga q se mueve con una velocidad v en el interior de un campo magnético B, actúa sobre ella la fuerza magnética Fm .
La dirección y el sentido de la fuerza magnética Fm viene dada por la regla de la mano derecha, girando de v hacia B.
La unidad en el Sistema Internacional (S.I.) del campo magnético es la Tesla (T). La fuerza hecha sobre una carga de 1 C que se mueve con una velocidad de 1 m/s perpendicularmente a un campo magnético de 1 T es de un Newton.
2.- MOVIMIENTO DE UNA CARGA PUNTUAL EN UN CAMPO MAGNÉTICO.
La fuerza magnética que actúa sobre una partícula cargada en movimiento en un campo magnético es siempre perpendicular a su velocidad. La fuerza magnética modificará la dirección de la velocidad pero no modificará su módulo. Así que, al no hacer trabajo sobre la partícula, no se modificará la energía cinética.
Si tenemos una partícula con una velocidad perpendicular a un campo magnético uniforme, la partícula describirá una trayectoria circular. La fuerza magnética es la responsable de la aceleración centrípeta necesaria para que haya un movimiento circular.
En estas condiciones, existe una relación entre el radio de la circunferencia formada por la trayectoria de la partícula y la masa m, la velocidad v, la carga q y el campo magnético B, la cual viene expresada de la siguiente forma :
r = m·v/q·B
2.- LAS FUENTES DEL CAMPO MAGNÉTICO.
Las primeras fuentes de campo magnético conocidas fueron los imanes permanentes. Los campos magnéticos formados por los imanes permanentes están entre 0.1 y 0.5 T.
En 1600, William Gilbert descubrió que la Tierra era un imán natural con polos magnéticos cerca de los polos geográficos. El campo magnético de la Tierra es de unos 10-4 T.
Otra fuente de campo magnético es el electroimán. Los electroimanes más potentes pueden llegar a producir campos magnéticos de hasta 2 T.
![]()
CUARTO APPLET :
El espectrómetro de masas
![]()
1.- HISTORIA BREVE.
El espectrómetro de masas fue diseñado por Francis William Aston en 1919 y mejorado por Kenneth BainBridge para medir la masa de los isótopos.
2.- ¿ Qué es un espectrómetro de masas ?.
El espectrómetro de masas se utiliza para determinar la relación masa-carga en iones de carga conocida, midiendo el radio de la órbita circular en presencia de un campo magnético conocido.
Esquemáticamente se podría decir que un espectrómetro de masas se compone de una fuente de iones, un campo eléctrico que se encarga de acelerar dichos iones y un campo magnético uniforme el cual produce la desviación de la trayectoria de los iones.
Los iones que provienen de la fuente de iones son acelerados a través de una diferencia de potencial y entran en un campo magnético uniforme y perpendicular. Los iones están obligados a seguir una trayectoria en forma de semicircunferencia a causa del campo magnético. Dichos iones acaban chocando con una placa fotográfica. Mirando la placa fotográfica podemos medir el radio de la trayectoria que han seguido los iones.
La ecuación r = mv/qB , nos da el radio r de la órbita de una partícula de masa m y carga q que se mueve con una velocidad v en presencia de un campo magnético B perpendicular a la velocidad de la partícula.
3.- ¿ Cómo hallar la masa de la partícula a partir del radio de la trayectoria descrita en la simulación ?.
La partícula es acelerada por una diferencia de potencial de V=5000 voltios. Tomaremos una partícula siempre de carga positiva con valor q=1.602177·10-19 C. La velocidad con que la partícula entrará en el campo magnético (B=0.1 T)será pues de :
1/2·m·v2 = q·V
v = ( 2qV / m )1/2
Como sabemos que el radio es igual a : r = mv/qB, sustituyendo la expresión de la velocidad citada antes en esta expresión del radio, tenemos que :
r2 = 2mV / qB2
Despejando la masa m de esta fórmula, tendremos que :
m = qB2r2 / 2V
Conociendo la carga q, el módulo del campo magnético B, el radio r y la diferencial de potencial V y aplicando la expresión anterior sabremos cual es la masa de la partícula.
4.- Datos sobre la conversión de gramos/mol a kg y viceversa.
En un mol hay 6.022·1023 átomos.
![]()