Suppose we want to know the electric field at the point due to point charges at fixed positions . We know that satisfies a supperposition principle and is given by:

where is the fixed location of the ith charge and is a constant that depends on the choice of units. In I.S. (Internacional System) of units, the charge can be measured with Coulombs (C) and the K constant is given by:

The constant is known as the electrical permitivity of free space. This choice of units is not convenient for computer programs because >>1. Another popular system of units is the Gaussian (cgs), system for which the constant is absorbed into the unit of charge, so that . Charge is in "electrostatic units" or "esu". One feature of Gaussian units is that the electric and magnetic fields have the same units. For example, the (Lorentz) force on a particle of charge and velocity in an electric field and a magnetic field has the form:

This virtues of the Gaussian system of units lead us to adopt this system for our application. The usual way of visualizing the electric field is to draw electric field lines. The properties of these lines are as follows:

• An electric field line is a directed line whose tangent at every position is parallel to the electric field at that position.

• The lines are smooth and continuous except at singularities such as point charges.

• The density of lines at any point in space is proportional to the magnitude of the field at that point. This property implies that the total number of a electric field lines from a point charge is proportional to the magnitude of that charge.

The application draws the electric field lines starting at positive charges if the net charge , or at negative charges if net charge . The program implements the following algorithm:

1. Begin at the point near a charge and compute the components of using the supperposition formula.
2. Draw a small line segment of size tangent to at that point. If then , otherwise . The components of the line segment are given by:

 

 



 

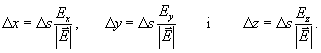
The program uses a small value for Ds if the field line is closed to the charges or if the magnitude is large. To speed up the program a large value of Ds is used when the field line moves off the screen and the field has a small magnitude.

3. Repeat the process beginning at the new point . Continue until the field line approaches another charge.
4. Repeat steps 1 to 3 for equally spaced starting positions on a circle around the charge. The spacing is inversely proportional to the magnitude of the charge.
5. Repeat steps 1 to 4 for each charge of the same sign.

PHYSICHAL FOUNDATIONS OF WAVEGUIDES

The communications world is based in information transmission using electromagnetic waves between a emitting and a receiver. We can divide this transmission into two basic types:

• Through a cable or a waveguide.

• Radiation of a electromagnetic waves through the air, free space or a dielectric material.

The searching of low attenuation channels and the need of sending signals with a wider band has produced that waveguides acquire an important place in the set of physical mediums used in communications. The cable television, the telephony, Internet, etc. have obligated to use more and more the waveguides, specially optical fibers.

Waveguide is called to any structure, or part of it, that allows the propagation of electromagnetic waves in a specified direction, being confinated in the transversal plane of propagation. The waves guiding is got due to the conection between fields and charges or current in the contours or by conditions of reflection in limits. Their origin is situated in the 30's when the radars and radio stations started to be used.

The structure and the waveguide's material constrution depens on the wave's frequence to carry. For microwave order frequencies are used open or closed systems by metallic conductors. In optical frequencies are used dielectrical waveguides.

If the frequency is high enough, all of them presents the common caracteristic of  having different configurations of electric and magnetic fields (called modes) which can propagate in the same waveguide at the same time, but with different velocities. The structure of these modes are often rather complicated and difficult to visualize due to its tridimensional structure.

The objective of this project is the graphic visualization of these modes for a rectangular waveguide with conductor walls.

It's necessary to comment also that all waveguides had a cutoff frequency under it, the transmission becomes impossible. This frequency is inversely proportional to waveguide transversal dimension. This produces the capability of transmitting signals from 1GHz (microwaves) because lower frequencies would need big dimensions.

The rectangular waveguide with conducting walls is the most important of waveguides with tube form. Consider a dielectric region  with wide a and height b and no limits in the Z axis direction and completely closed by conducting walls.

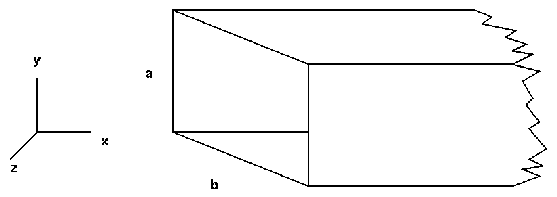
Solving the Maxwell equations under the contour conditions given by the characteristics of a rectangualar waveguide we can find the modes. We suppose there are no losses in the dielectric zone and then the electric current density is null . The dependency in position and time of fields we consider is:

where we use the complex notation and the + (-) means a electromagnetic wave propagation in positive (negative) sense of Z axis z.

The Maxwell equations wich govern the behaviour of waves are:

where are respectively the electric field, the vector of magnetic induction, the magnetic field and the electric displacement. From these equations we arrive to the vectorial wave equations:

where are the electric permisivity and the magnetic permeability of dielectric medium, respectively.

The solutions of these equations can be decomposed in types called modes and can be in general:

• Transversal magnetic modes (TM) in which .

• Transversal electric modes (TE) in which .

• Transversal electromagnetic (TEM) in which and .

In the empty waveguide like we are studying is demonstrable that don't exist the TEM modes, which are otherway the most usuals in systems with two conductors like coaxial cables.