Si dessitjem conèixer el camp elèctric al punto producït per càrregues puntuals a les posicions fixes . Sabem quesatisfà el principi de superposició, que s'expresa com:

on és la localització fixa de la càrrega i-ésima i és una constant que depèn de les unitats triades. Al S.I. (Sistema Internacional) d'unitats, la càrrega es medeix en Coulombs (C) i la constant K ve donada com:

La constant és la permisivitat elèctrica del buit. Aquesta selecció no és molt convenient per el càlcul amb ordinador ja que >>1. Un altre sistema d'unitats és el Gaussià (cgs), pel qual, la constant és absorvida dins de l'unitat de càrrega, tenint llavors . La càrrega s'expresa donç en unitats electrostàtiques o "esu". En aquest sistema els camps elèctrics i magnètics tenen les mateixes unitats. Per exemple, la força sobre una partícula amb càrrega i velocitat que es mou dins d'una zona amb un camp elèctrici un camp magnètic, s'expresa :

Aquestes característiques del sistema Gaussià d'unitats ens indueixen a adoptar-lo com sistema d'unitats per realizar la nostra aplicació. La manera habitual utilitzada per visualitzar camps elèctrics és dibuixar les línies del camp elèctric. Les propietats de les esmentades línies són les següents:

• Una línia de camp elèctric és una línia tal que la tangent a la mateixa, en qualsevol punt, és paral.lela al camp elèctric existent a aquella posició.

• Les línies són uniformes i continues amb origen a les càrregas positives i final a les negatives.

• La densitat de líneas a un punt qualsevol de l'espai és proporcional a la magnitud del camp en aquell punt. Aquesta propietat implica que el número total de línies del camp elèctric des d'un punt amb càrrega és proporcional a la magnitut de la càrrega.

L'aplicació dibuixa les línies de camp elèctric començant per les càrregues positives si , o per les càrregues negatives si . El programa implementa el següent algorisme:

1. S'inicia a un punt proper a una càrrega i computa les components del vector del camp elèctric al punt utilitzant la primera fórmula descrita.
2. Es dibuixa un petit segment de línia de mesura tangent a al punt. Si llavors , d'una altra manera . Les components del segment de línia venen donats com:

 

 



 

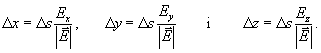
El programa usa un D s petit si la línia de camp està a prop de les càrregues o si la magnitut del camp és gran. Amb l'objectiu d'accelerar el programa, s'utilitza un valor gran per D s quan una línia de camp es mou fora de la pantalla i la magnitut del camp és petita.

3. El procès es repeteix des del principi a partir del punt, i continúa fins que la línia de camp s'aproxima a una altra càrrega.
4. Els pasos 1,2 i 3 es repeteixen per punts equidistants a un cercle al voltant de la càrrega, on la distància és inversament proporcional a la magnitut de la càrrega.
5. Es repetirà per cada una de les càrregues del mateix signe els pasos 1,2,3 i 4.

FONAMENTS FÍSICS DE LES GUIES D'ONES

El món de les comunicacions està basat a la transmissió d'informació mitjançant ones electromagnètiques (OEM) entre un emissor i un receptor. Fonamentalment podem dividir aquesta transmissió en dos tipus fonamentals:

• A travès d'un cable o guia d'ones (GdO).

• Radiació d'OEM a travès de l'aire, l'espacio lliure o d'un medi dielèctric.

La recerca de canals amb baixa atenuació i la necessitat d'enviar senyals amb una amplada de banda cada vegada més gran ha fet que les GdO, que són l'objecte d'estudi d'aquest projecte, juguin un paper cada vegada més important  al conjunt dels mitjans físics per la comunicació. La televisió per cable, la telefonía, Internet, etc. obliguen a un ús cada vegada més gran de GdO, en particular de fibres óptiques.

S'anomena GdO a qualsevol estructura, o part d'una estructura, que fa que una OEM es propagui en una direcció determinada, amb algun grau de confinament al pla transversal a la direcció de propagació. El guiat de les ones s'aconsegueix degut a la conexió entre els camps i les càrregues o corrents als contorns o bé per condicions de reflexió als límits. El seu origen es sitúa als anys 30 quan es van començar a utilitzar a radars i emissores de ràdio de freqüències de microones.

L'estructura i el material de construcció de les GdO depèn de la freqüència de les oes que han de transportar. Per freqüències de l'ordre de les microones són habitualment sistemes oberts o tancats de conductors metàl.lics. A freqüències óptiques s'utilizen GdO dielèctriques.

Totes elles presenten la característica comú de que, si la freqüència és suficientement alta, diverses configuracions dels camps elèctric i magnètic (els anomenats modes) es poden propagar a la mateixa guia simultàneament, encara que amb diferents velocitats. L'estructura d'aquests modes és sovint bastant complicada i difícil de visualitzar degut a la seva estructura tridimensional.

L'objectiu d'aquest projecte és precisament la visualització gràfica d'aquests modes per una guia d'ones rectangular de parets conductores.

És necessari comentar també que totes les GdO tenen una freqüència de tall per sota de la qual la transmissió és impossible. Aquesta freqüència és inversament proporcional a la dimensió transversal de la guia. Això produeix que siguin factibles per la transmissió de senyals de freqüències a partir de 1GHz (microones) ja que a freqüències menors requeririen unes dimensions massa grans.

La GdO rectangular de parets conductores és la més important de les GdO en forma de tub. Considerem una regió dielèctrica d'amplada a i alçada b que s'estèn indefinidament a la direcció axial (z) i que està totalment tancada per parets conductores.

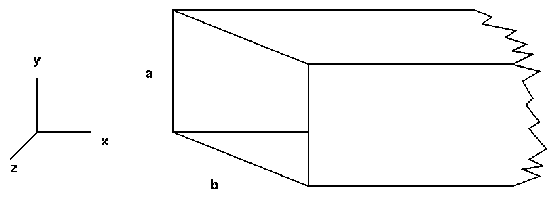
Amb l'objectiu de trobar els modes de la GdO s'ha de trobar la solució de les equacions de Maxwell sota les condicions de contorn imposades per les característiques de la guia. Se suposa que la regió dielèctrica limitada pels conductors no té pérdues i per tant la densitat de corrent elèctric al seu interior és nul.la, . La dependència en la posició i el temps dels camps que considerem és:

on utilitzem l'habitual notació complexa i el superíndex + (-) indica una OEM que es propaga al sentit positiu (negatiu) de l'eix z.

Les equacions de Maxwell que governaran el comportament de les ones són:

on són respectivament el camp elèctric, el vector d'inducció magnètica, el camp magnètic i el desplaçament elèctric. A partir d'aquestes equacions s'arriva a les equacions d'ona vectorials:

on són la permisivitat elèctrica i la permeabilitat magnètica del medi dielèctric, respectivament.

Les solucions d'aquestes equacions es poden descomposar en clases que reben el nom de modes i que poden ser, en general, dels sigüents tipus:

• Modes transversals magnètics (TM) als quals .

• Modes transversals elèctrics (TE) als quals .

• Modes transversals electromagnètics (TEM) als que tant com .

A les GdO buides com les que estudiarem aquí es pot demostrar que no existeixen els modes TEM, que d'altra banda són els dominants als sistemes de dos conductors, com els cables coaxials.